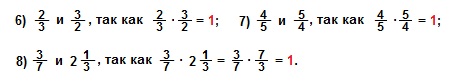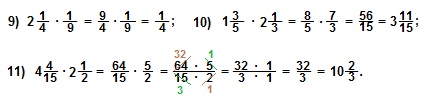На предыдущих уроках мы узнали как складывают и вычитают обыкновенные дроби и смешанные числа. Помните, в самом начале нам казалось это очень сложным. Дроби к общему знаменателю приведи, а это, пожалуй, и есть самое сложное, полученную дробь сократи, результат в виде смешанного числа представь. Неужели с умножением и делением все также сложно? К счастью, нет. Как показывает практика, умножать обыкновенные дроби и делить их у ребят получается намного лучше, чем складывать и вычитать их. Понятно, что в результате умножения двух дробей, должна получиться обыкновенная дробь. Но что нам записать в числителе этой дроби, а что в знаменателе? Давайте поскорее разберем, как же найти произведение двух обыкновенных дробей.
И так, когда мы только приступали к арифметическим действиям с обыкновенными дробями вы высказывали предположения относительно правил сложения и вычитания дробей. Одно из предположений звучало так: числитель складываем с числителем, знаменатель со знаменателем. Относительно сложения и вычитания обыкновенных дробей это предположение неверно, а вот умножение именно так и выполняется. Неужели все так просто? Числитель умножаем на числитель, а знаменатель на знаменатель? Да, все так просто. Произведение числителей записывают в числитель, а произведение знаменателей в знаменатель. Можем записать это правило в буквенном виде.
$\frac{a}{b}$ * $\frac{c}{d}$ = $\frac{a*c}{b*d}$
Произведением двух обыкновенных дробей являеся дробь, в числителе которой записано произведение числителей, а в знаменателе - произведение знаменателей.
А теперь разберем примеры.
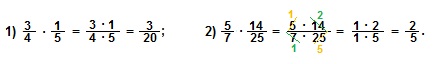
Стоп, почему во втором примере мы не умножали числители и знаменатели, так как обговаривали? Вернее, почему мы вдруг решили сократить числители и знаменатели? Так нужно делать каждый раз? Да, мы должны сокращать дробь. Но у нас два пути, и каждый из нас может выбрать тот путь, по которому ему удобнее двигаться. Мы можем сокращать дробь, которая получилась в результате умножения двух дробей, т.е. сокращать результат, либо сокращать на промежуточном шаге, т.е. в процессе, как было показано в предыдущем примере. Однако здесь нужно учитывать, что сокращать можно только те числа, которые находятся по разные стороны от дробной черты, мы обязательно должны взять одно число из числителя и одно из знаменателя. Нельзя брать и сокращать, например, два числа из числителя, или два числа из знаменателя. Каким из этих двух путей идти, каждый решит сам. Может быть сокращение в процессе вычислений облегчает сам процесс подсчета числителя и знаменателя конечной дроби, особенно если нужно выполнить умножение трех, четырех, или пяти дробей. Да, да, часто ставятся задачи, где умножать нужно будет не пару дробей, а больше.
С умнжением обыкновенных дробей разобрались, а что делать, если нужно умножить обыкновенную дробь на натуральное число. Вспомним, что любое натуральное число можно предствить в виде дроби, со знаменателем единица, т.е. в виде n=$\frac{n}{1}$. Получается, если перед нами стоит задача найти произведение обыкновенной дроби и натурального числа, то мы должны найи произведение этой обыкновенной дроби и обыкновенной дроби $\frac{n}{1}$, где в числителе записано натуральное число. Если после этого воспользоваться правилом умножения обыкновенных дробей, то станет понятно что числитель обыкновенной дроби будет умножен на натуральное число, а знаменатель на единицу. Тогда, чтобы найти произведение обыкновенной дроби и натурального числа, нужно числитель обыкновенной дроби умножить на это натуральное число, а знаменатель оставить без изменений.
Примеры.
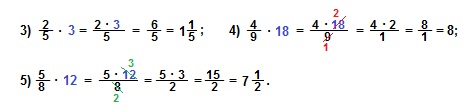
Опять же, мы можем сокращать в процессе, а можем сократить полученный результат.
А как умножить два смешанных числа? Также как и при сложении - целое с целым, дробное с дробным? А если быть точным, целую часть умножить на целую, а дробное на дробую? Нет, умножение смешанных чисел производится по другим правилам. Умножать обыкновенные дроби, как мы помним, достаточно легко. Значит, мы должны максимально приблизить то что нам дано - смешанные числа, к тому, с чем нам легко работать - обыкновенные дроби. Вспомним, что любое смешанное число можно представить в виде неправильной дроби. Значит, прежде чем умножать смешанные числа, их нужно обратить в неправильные дроби и после этого выполнить умножение двух обыкновенных дробей. Если в результате умножения получится неправильная дробь, то ее вновь нужно перевести в смешанное число
III. Два числа, произведение которых равно единице, называют взаимно обратными числами.
Примеры взаимно обратных чисел: