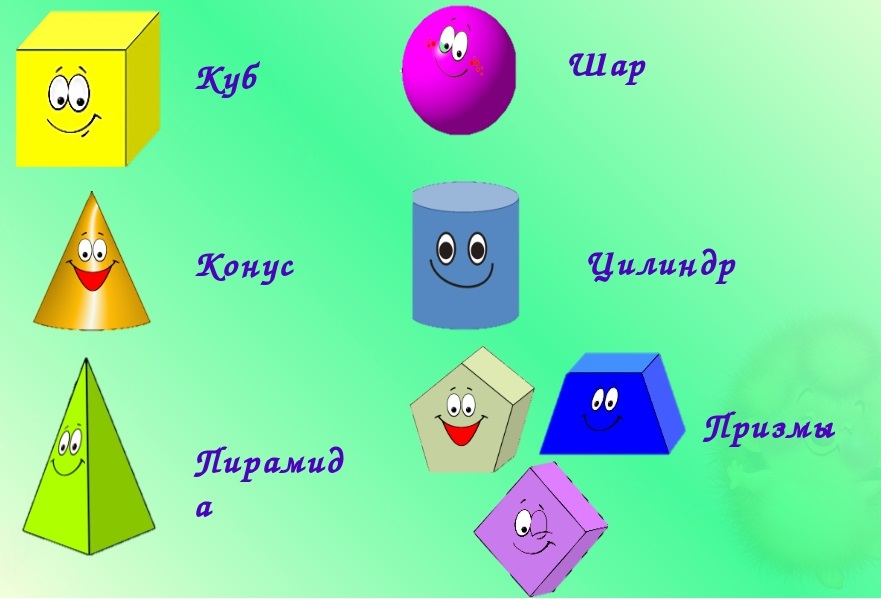
Нас окружает множество предметов, но математиков интересуют лишь форма предметов и их размеры, поэтому вместо предметов они рассматривают геометрические тела. Вы, конечно, знаете уже некоторые геометрические тела: шар, параллелепипед, куб. А с некоторыми только начинаете знакомство: цилиндр, конус, призма. Оглянитесь, вокруг находится множество объектов, которые имеют форму геометрических тел. Например, шкаф "похож" на прямоугольный параллелепипед, сахар рафинад на куб, карандаш - цилиндр, яблоко - шар.
Поверхность любого геометрического тела делит пространство на две области: внутреннюю и внешнюю (мы уже упоминали эти слова, когда говорили о замкнутых линиях, которые также делили плоскость на две: внутреннюю и внешнюю). Как не трудно догадаться из названия, всё что находится "внутри" геометрического тела образует внутреннюю область, а всё что снаружи - внешнюю. Если мы возьмем шкаф, как объект, имеющий форму параллелепипеда, то всё, что внутри него (одежда, полотенца, постельное белье, обувь), будет внутренней областью, а комната, дом, улица и вы - будет относится к внешней области. Но если вдруг, во время игры в прятки с младшей сестрой, вы решите спрятаться в шкаф, то станете уже частью внутренней области.

Хорошо, а существуют ли названия у поверхностей геометрических тел? Оказывается, что особое название имеет лишь поверхность шара. Ее называют сферой («сфера» — латинская форма греческого слова «сфайра» —шар). Если в качестве модели шара взять апельсин, то становится понятно, что кожура разделяет пространство на внутреннюю область (дольки) и внешнюю, кожура - поверхность апельсина - сфера. Значит шар и сфера понятия разные (аналогично, когда речь идет о геометрических фигурах разными понятиями являются окружность и круг). Остальные геометрические тела не имеют названия поверхности.

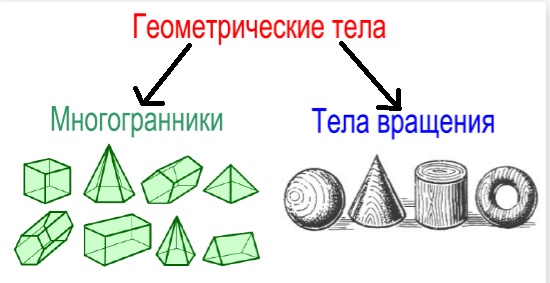
Всё множество геометрических тел в математкие разделяют на две группы: тела вращения и многогранники. Что такое тела вращения? Если говорить простым языком, тело вращения - это геометрическое тело, которое не имеет "острых углов". К этой группе относятся те геометрические тела, которые имеют в качестве одной из граней круг: цилиндр, конус, и самое "безопасное" геометрическое тело (потому что вообще не имеет углов) - шар. Геометрические тела, которые не имеют в своем составе круга, называются многогранниками: параллелепипед, куб, пирамида. Многогранник – геометрическое тело, ограниченное со всех сторон плоскими многоугольниками.

Первые упоминания о многогранниках известны еще за три тысячи лет до нашей эры в Египте и Вавилоне. Но теория многогранников является и современным разделом математики. При всём многообразии многогранников у них имеются ряд общих свойств:
1) Поверхность многогранника состоит из многоугольников.
2) Каждый из этих многоугольников называется гранью многогранника.
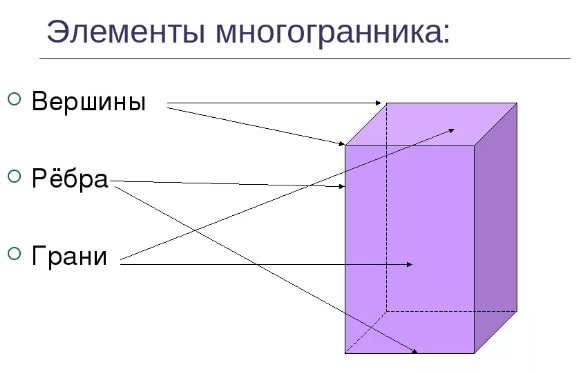
3) Вершины этих многоугольников являются также и вершинами многогранника, а стороны многоугольников – рёбрами многогранника.
Запомни! Вершины - это точки.
Ребра - отрезки, соединяющие эти точки (вершины).
Грани - это многоугольники.
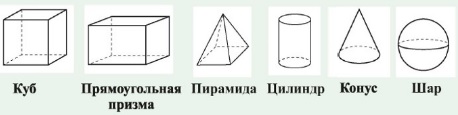
С давних пор люди искали различные способы изображения объёмных тел, передающее ощущение глубины пространства. Были разработаны специальные приёмы, позволяющие обмануть зрение. Например, пунктирными линиями в математике изображают невидимые ребра многогранников.
Тренировочные задания по теме "Геометрические тела и многогранники"
