Деление обыкновенных дробей

Деление дроби на дробь

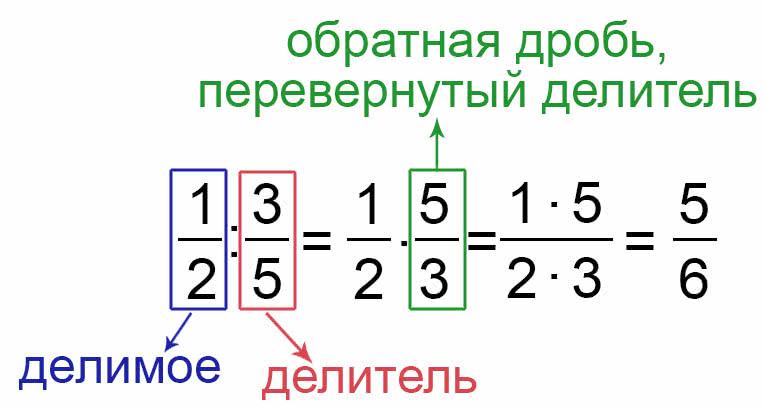
Чтобы делить дробь на дробь, нужно дробь, которая является делителем перевернуть, то есть получить обратную дробь делителю и потом выполнить умножение дробей.

$\frac{a}{b}$÷$\frac{c}{d}$=$\frac{a}{b}$*$\frac{d}{c}$

Пример:

Выполните деление обыкновенных дробей

Деление дроби на число.

Чтобы разделить дробь на число, нужно знаменатель дроби умножить на число.

$\frac{a}{b}$÷n=$\frac{a}{b}$÷$\frac{n}{1}$=$\frac{a}{b}$ × $\frac{1}{n}$

Рассмотрим пример:

Выполните деления дроби на натуральное число $\frac{4}{7}$ ÷3.

Как мы уже знаем, что любое число можно представить в виде дроби  3=$\frac{3}{1}$.

$\frac{4}{7}$÷3=$\frac{4}{7}$÷$\frac{3}{1}$=$\frac{4}{7}$×$\frac{1}{3}$=$\frac{4*1}{7*3}$=$\frac{4}{21}$.

Деление числа на дробь

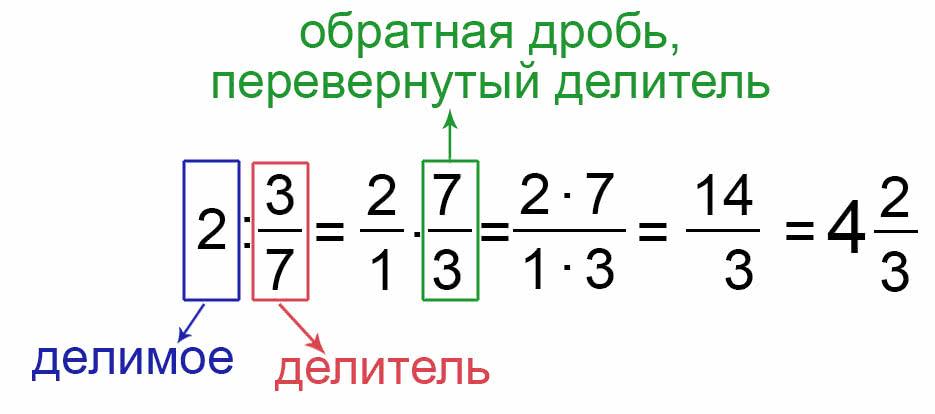
Чтобы поделить число на дробь, нужно знаменатель делителя умножить на число, а числитель делителя записать в знаменатель. То есть дробь делитель перевернуть.

Рассмотрим пример:

Выполните деление числа на дробь.

Деление смешанных дробей.

Перед тем как приступить к делению смешанных дробей, их нужно перевести в неправильную дробь, а дальше выполнить деление по правилу деления дроби на дробь.

Пример:

Выполните деление смешанных дробей.

2$\frac{3}{4}$÷3$\frac{1}{6}$=$\frac{11}{4}$÷$\frac{19}{6}$=$\frac{11}{4}$×$\frac{6}{19}$=$\frac{11*6}{4*19}$=$\frac{11*3}{2*19}$=$\frac{33}{38}$

Деление числа на число.

Чтобы поделить простые числа, нужно представить их в виде дроби  и выполнить деление по правилам деления дроби на дробь.

Пример:

2÷5=$\frac{2}{1}$÷$\frac{5}{1}$=$\frac{2}{1}$×$\frac{1}{5}$=$\frac{2*1}{1*5}$=$\frac{2}{5}$

На нуль делить нельзя.

Может возникнуть вопрос: как делить дроби с разными знаменателями?

Ответ: не важно одинаковые или разные знаменатели у дробей, все дроби делятся по правилу деления дроби на дробь.

Проверочный тест "Деление обыкновенных дробей"